今天我們要介紹用來提升查詢效率的WAND演算法。

在這個演算法中我們會為每一個字詞記錄一個數值，這個數值稱為maximum contribution。一個字詞的maximum contribution記下了這個字詞在所有文件中可能獲得的「最高」分數。舉例來說，包含字詞"him"的所有文件分別為Doc1, Doc2以及Doc4，Doc1有2.4分、Doc2有3.3分、Doc4有0.8分，那字詞"him"的max contribution就是3.3分。

在運算上，我們會隨時記錄著top-k高分的文件，同時我們會跳過每一個沒辦法進入top-k列表中的文件。舉例來說，我們想查詢"The quick brown fox"這句話，設定找出top-2的文件：

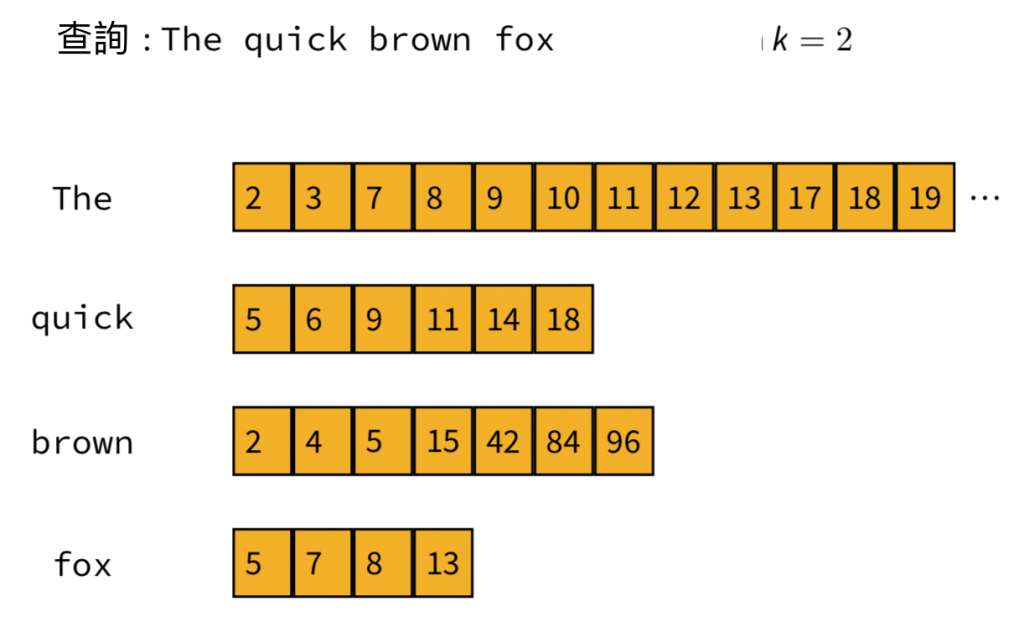
我們首先記下每個字詞的maximum contribution：

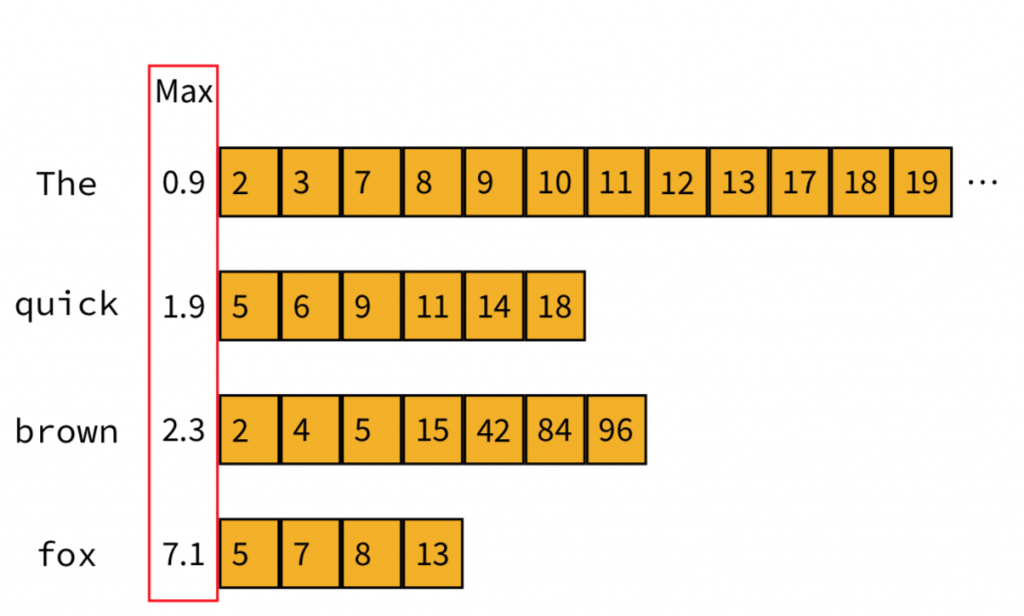
首先將指標指向最前面的文件

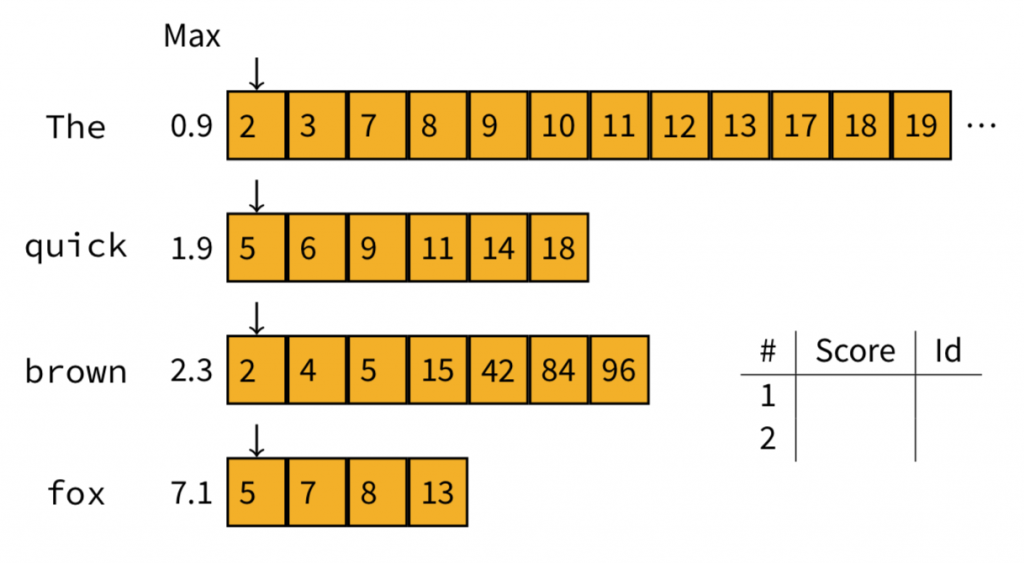
接著，我們調整一下字詞的順序（Doc2裡面也有出現brown，所以把它排上來）。計算之後我們發現，雖然"The"跟"brown"的maximum contribution相加是3.2，但實際分數卻是2.0，所以我們就記錄這分數。

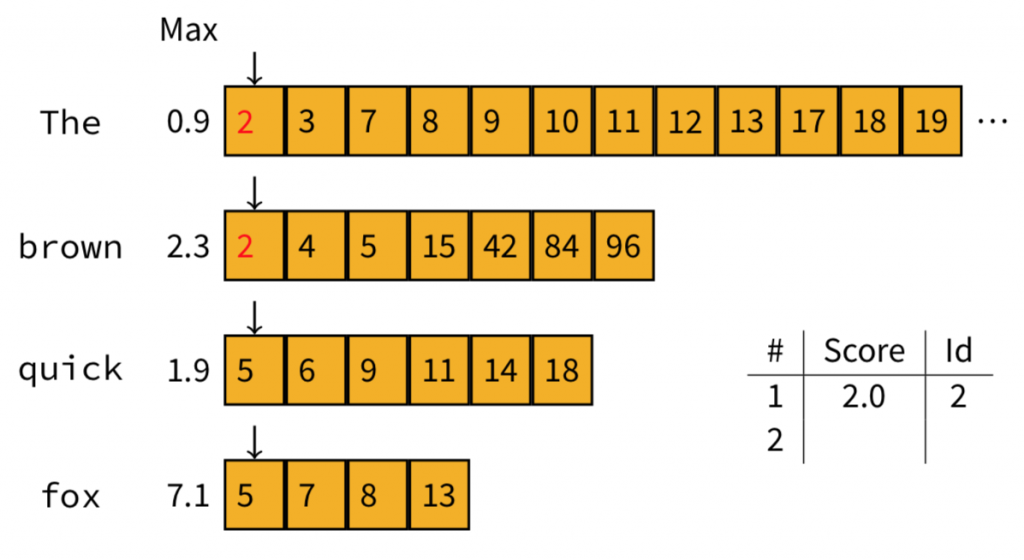
再來，我們將指標移到下一個文件

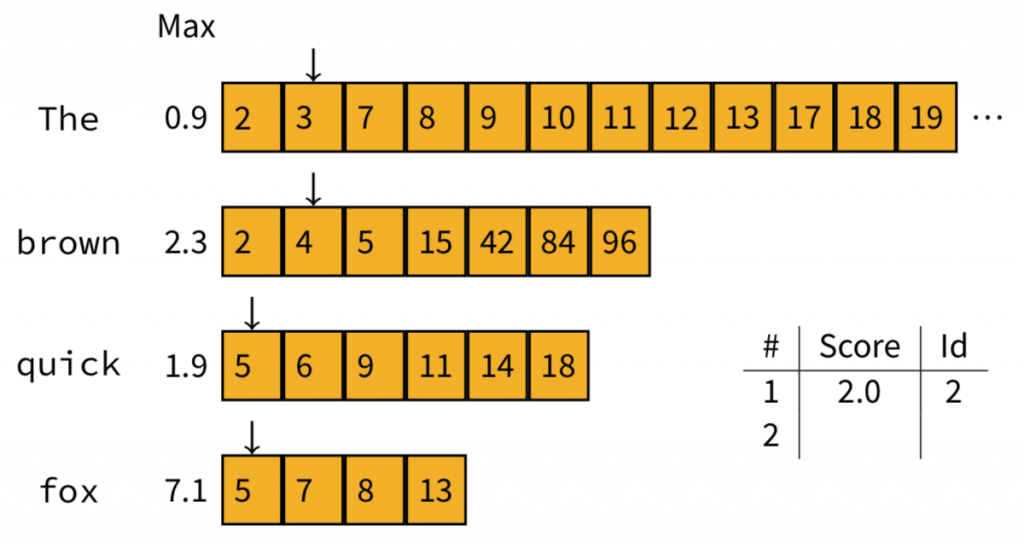
計算後我們發現，Doc3的分數是0.5，仍在Top-2裡面，所以放到榜上

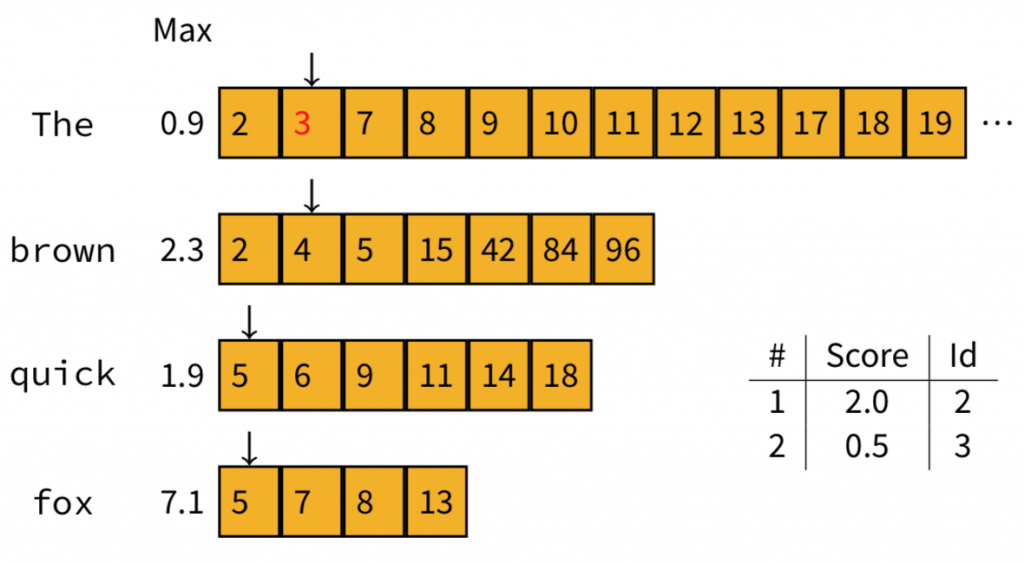
Doc4只有"brown"這個字詞，所以我們重排顯示的順序

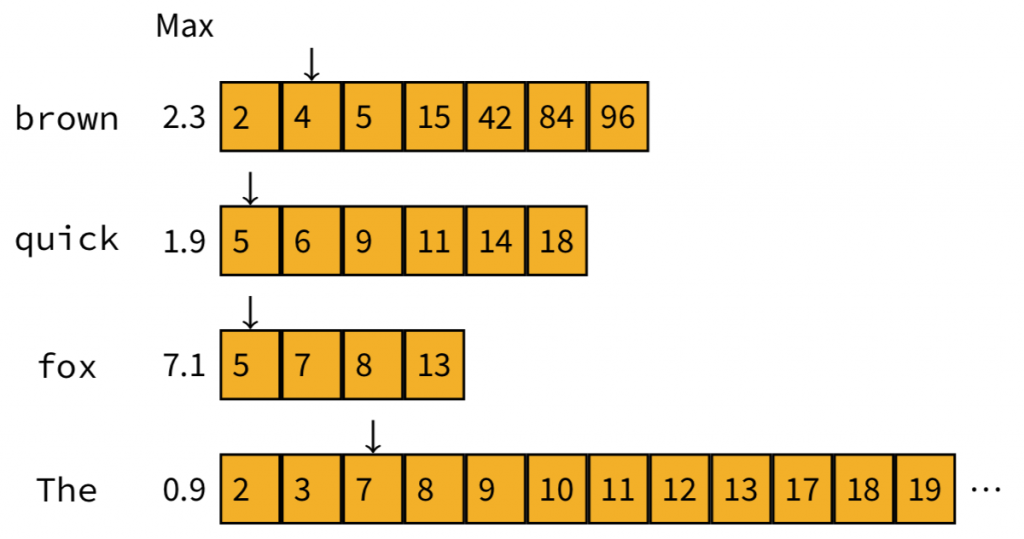
這時我們察覺，Doc4的maximum contribution加起來（也就只有brown自己）是2.3分，高過top-2榜單上的第二位，所以我們需要加以計算，決定Doc4能不能進到榜單當中。

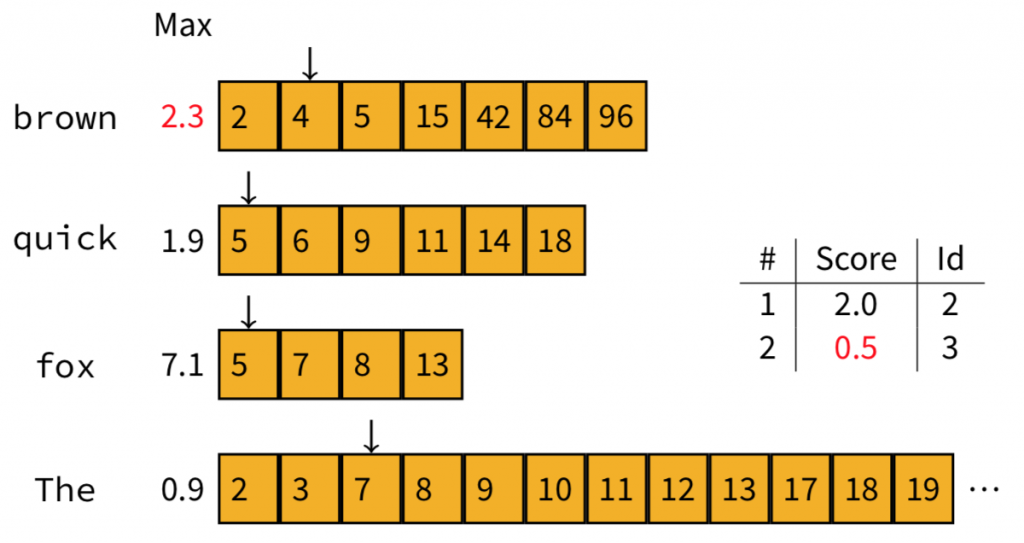
計算的結果是：Doc4獲得1.4分，仍然高過Doc3的0.5分，因此，我們用Doc4取代Doc3。

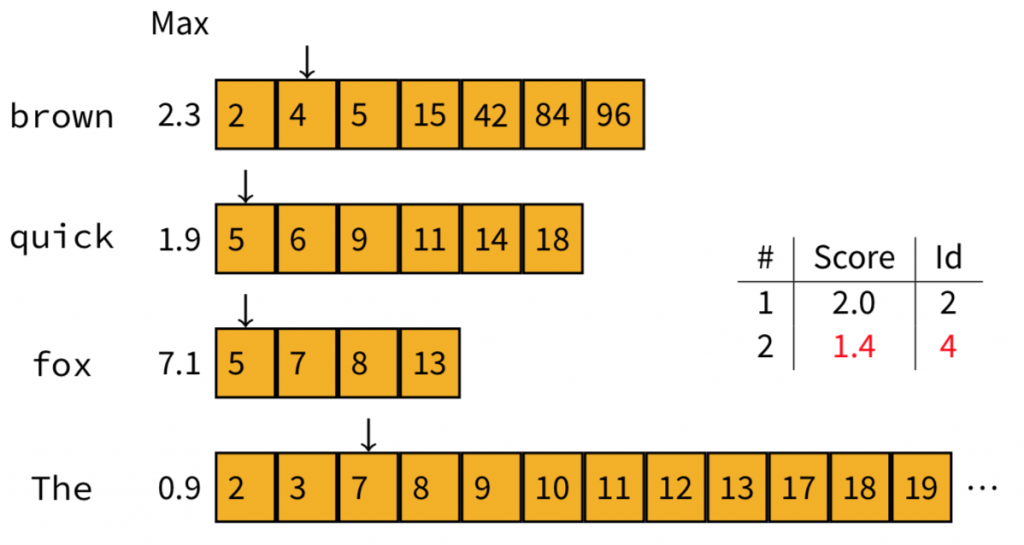
到了Doc5，因為它的max contribution是2.3+1.9+7.1=11.3，大於Top-2的第二名(1.4)，所以我們需要計算它的實際分數。計算出來的結果，Doc5分數為6.3，已經高於Top-2榜單的第一名了，因此我們把它放到第一位，原本的第一位也就擠到第二位，而原來的第二名就被擠出榜單之外了。

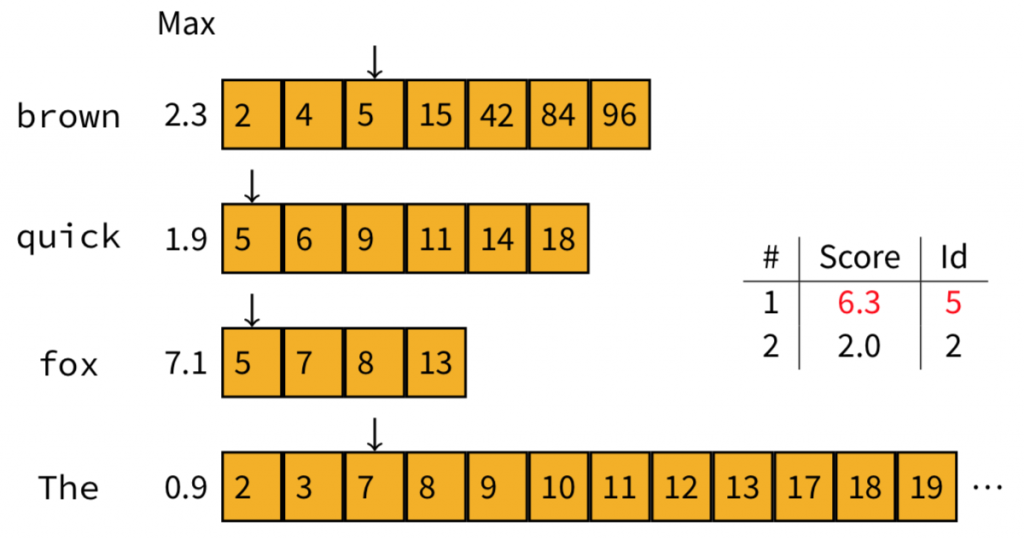
我們繼續移動指標

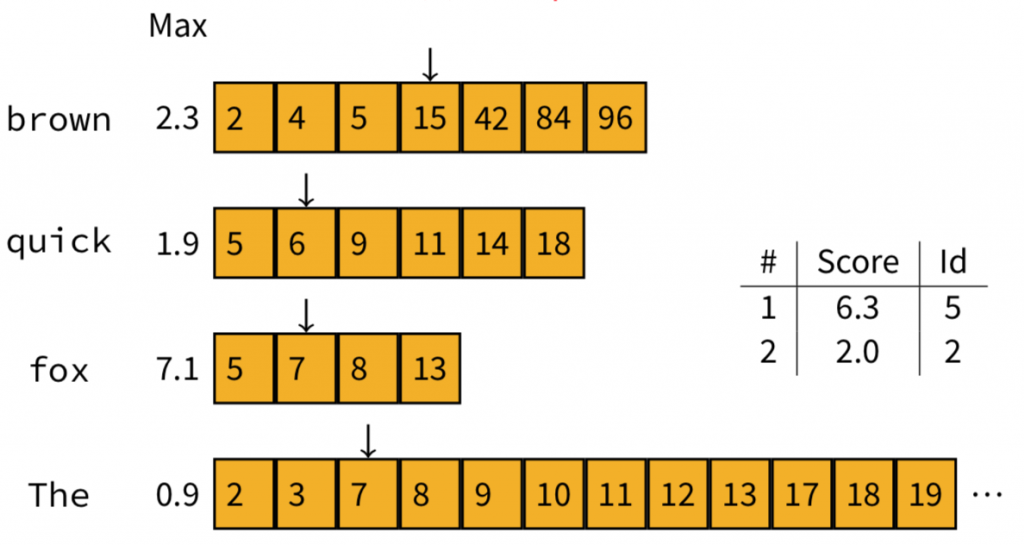
發現Doc6的max contribution相加僅有1.9，小於榜單的第二位(2.0)，因此我們跳過它，不進行計算

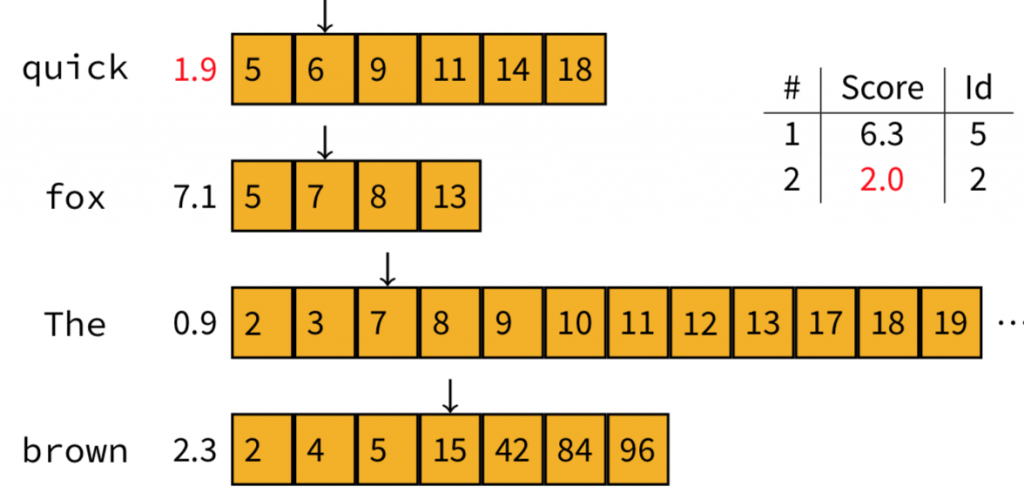
我們加快進行，Doc7的分數為8.1，因此放入榜單中。Doc8雖然max contribution高過6.3，但計算後發現分數不到6.3，因此沒有進到榜單裡。到了Doc9，它的max contribution相加只有2.8，低於榜單的最後一位（第二名），因此我們連計算都不需要計算，直接跳過它。

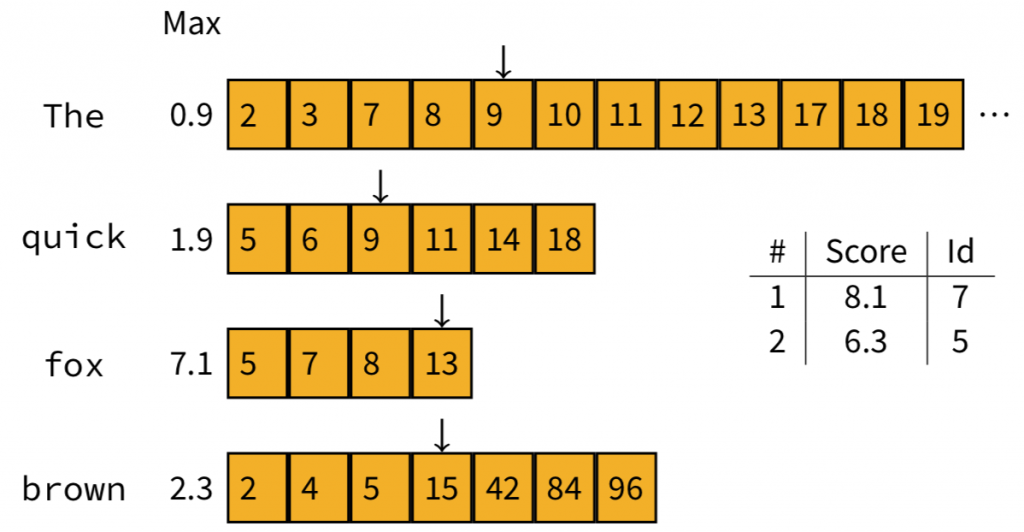
這時我們也可以想想，下一個要計算的文件是哪一個？答案是Doc13，因為前面幾個的max contribution相加都不會高過6.3，所以都是我們可以省略的部分，直到Doc13，它相加的分數為8.0，這時我們才需要計算它的實際分數。

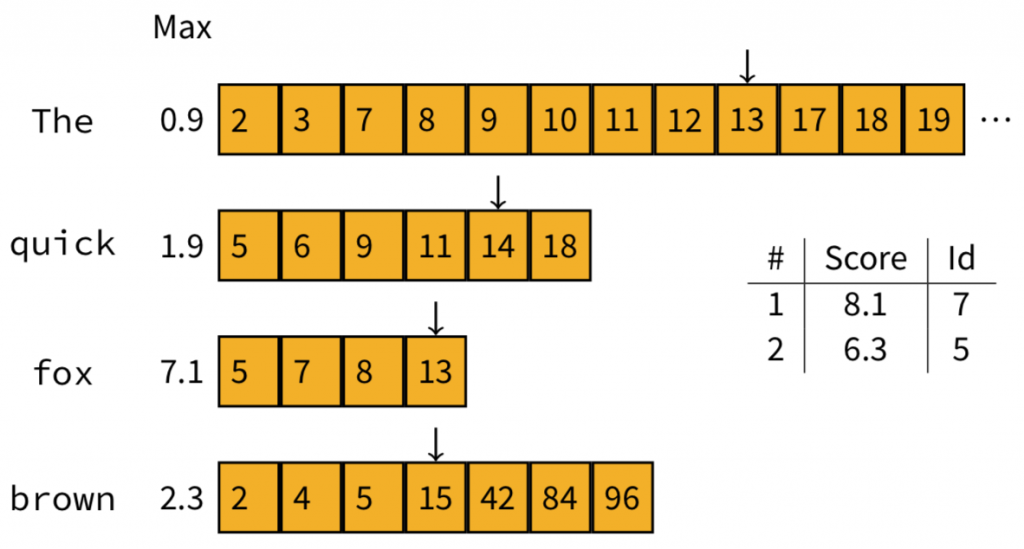
假設Doc13最後計算出來的分數不高於6.3，它就不會進到榜單中。那麼，請問下一個會被計算的文件是哪一個呢？